This post presents the last of the six postulates of quantum mechanics. Up to now, we have seen how a quantum mechanical state is defined, what is the outcomes of measurements on such systems, and how measurements affect them. The sixth postulate determines how quantum mechanical system evolve in time; it defines the equation of motion of quantum mechanics.
Postulate VI: The evolution of the system is given by the time-dependent Schrödinger equation:
(1)
where
and
are the state of the system and the Hamiltonian operator at time
, respectively. The Hamiltonian is defined as the operator representing the total energy of the system.
The Hamiltonian is often split into two terms: the kinetic energy of the particles and the potential energy, which can contain many different contributions (e.g.: due to interactions with electric and magnetic fields). From the perspective of magnetic resonance, only the potential energy term usually matters. That’s where spin-field and spin-spin interactions are encoded.
We note that, because we chose in a previous post to express operators in angular frequency units rather than in Joules, the time-dependent Schrödinger equation reads
(2) ![]()
This choice doesn’t affect the definition of the states. However, it does affect the units of the eigenvalues for the Hamiltonian. If ![]() is an eigenvalue of
is an eigenvalue of ![]() expressed in Joules, then
expressed in Joules, then ![]() is the corresponding eigenvalue of
is the corresponding eigenvalue of ![]() expressed in rad/s. They are related by
expressed in rad/s. They are related by ![]() .
.
We will not go into a lot of details on how Hamiltonian operators are constructed and where they come from in this post. But I just want to mention the so-called correspondence principle, which is used to this end, and illustrate it with an example. Let’s take a single spin interacting with a static magnetic field ![]() along the
along the ![]() axis. In classical terms, the spin has a magnetic moment
axis. In classical terms, the spin has a magnetic moment ![]() , where
, where ![]() is the gyromagnetic moment of the spin and
is the gyromagnetic moment of the spin and ![]() is the spin angular momentum. Still in classical terms, the energy associated with the interaction of this spin with the magnetic field is given by
is the spin angular momentum. Still in classical terms, the energy associated with the interaction of this spin with the magnetic field is given by
(3) 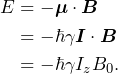
According to the correspondence principle, the Hamiltonian corresponding to this interaction is obtained by replacing the classical quantities (or observables) in the expression for the energy by the corresponding quantum mechanical operators.
(4) 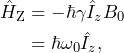
expressed in Joules, where ![]() is called the Larmor frequency of the spin.
is called the Larmor frequency of the spin. ![]() and
and ![]() are constants so they are not replaced by an operator, while
are constants so they are not replaced by an operator, while ![]() is a property of the spin, i.e., a quantum mechanical object, so it is replaced by the corresponding operator
is a property of the spin, i.e., a quantum mechanical object, so it is replaced by the corresponding operator ![]() . This particular Hamiltonian is called the Zeeman Hamiltonian, as it gives rise to the Zeeman splitting. Expressed in units of rad/s, it reads
. This particular Hamiltonian is called the Zeeman Hamiltonian, as it gives rise to the Zeeman splitting. Expressed in units of rad/s, it reads
(5) ![]()
The correspondence principle can be used to construct operators of all sorts but, most of the time, we will take the expression as a fact.
Now that we have determined the Hamiltonian describing the interaction of a spin with a static magnetic field, we can use the time-dependent Schrödinger equation to determine how specific spin states will evolve under the effect of the magnetic field. Let’s calculate how a spin in the states
(6) 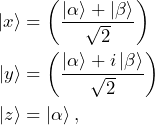
evolves under the effect of the Zeeman Hamiltonian ![]() . If, at time
. If, at time ![]() , the system is in state
, the system is in state ![]() , i.e., aligned along the magnetic field, it will evolve as
, i.e., aligned along the magnetic field, it will evolve as
(7) 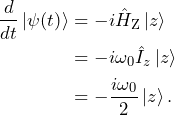
The solution to this differential equation with ![]() is
is
(8) ![]()
This shows that the spin parallel with the magnetic field does not evolve in time, except for the term ![]() , which is called the phase factor, with
, which is called the phase factor, with ![]() being the global phase of the system. The global phase has little practical implications as it does not affect the expectation values of
being the global phase of the system. The global phase has little practical implications as it does not affect the expectation values of ![]() for any observable operator
for any observable operator ![]()
(9) 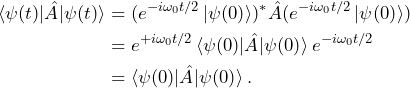
More interesting things happen if the spin is aligned is in the ![]() or
or ![]() states at time
states at time ![]() , i.e., perpendicular to the magnetic field. For
, i.e., perpendicular to the magnetic field. For ![]() , the system evolves as
, the system evolves as
(10) 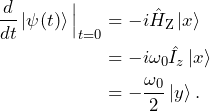
For ![]() , the system evolves as
, the system evolves as
(11) 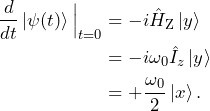
In the calculations above we made use of the following equalities
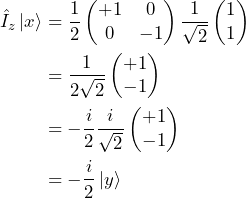
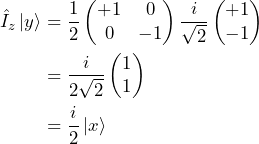
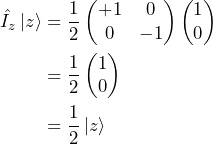
Now, what does this mean? When the spin is aligned with the magnetic field it does not change. When the spin is perpendicular to the magnetic field however, Eq. 10 tells us that ![]() turns into
turns into ![]() and Eq. 11 tells us that
and Eq. 11 tells us that ![]() turns into
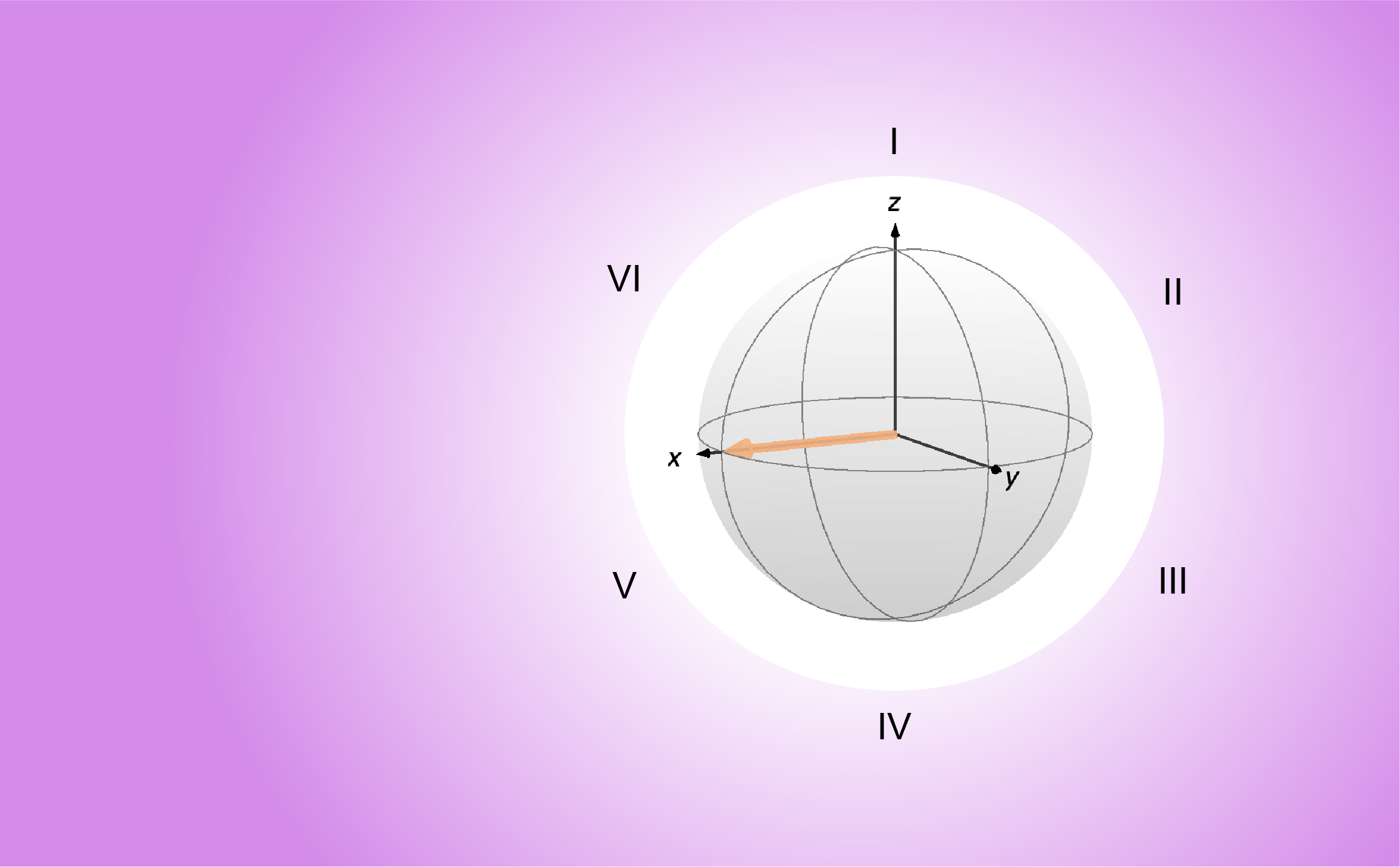
turns into ![]() . In other words, the transverse component of the spin angular momentum precesses about the magnetic field.
. In other words, the transverse component of the spin angular momentum precesses about the magnetic field.
Before concluding this post, let’s take a closer look at state ![]() . We saw that
. We saw that ![]() does not evolve under the effect of the Zeeman Hamiltonian (except for the global phase factor). States that do not evolve under the effect of the Hamiltonian are of particular interest. They are called stationary states. That a state
does not evolve under the effect of the Zeeman Hamiltonian (except for the global phase factor). States that do not evolve under the effect of the Hamiltonian are of particular interest. They are called stationary states. That a state ![]() is stationary under the Hamiltonian (that does not change with time) is equivalent to that state being an eigenstate of the Hamiltonian
is stationary under the Hamiltonian (that does not change with time) is equivalent to that state being an eigenstate of the Hamiltonian
(12) ![]()
expressed in Joules, where we see from the third postulate that ![]() must be the expectation value of the energy associated with
must be the expectation value of the energy associated with ![]() ,
,
(13) ![]()
Eq. 12 is called the time-independent Schrödinger equation. Expressed in rad/s, the time-independent Schrondinger equation reads
(14) ![]()
with
(15) ![]()
If ![]() is a stationary state, the state as a function of time is written as
is a stationary state, the state as a function of time is written as ![]() . We plug in this expression into the time-dependent Schrödinger equation and get
. We plug in this expression into the time-dependent Schrödinger equation and get
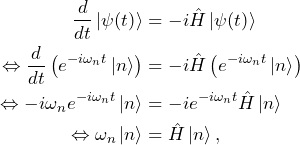
which is the time-independent Schrödinger equation.
Because of Eq. 9, we know that the phase factor will not bring much useful information. It is a common practice to define a projective Hilbert space ![]() , where each subspace of states in
, where each subspace of states in ![]() which differ only by a phase factor are identified to a single point in
which differ only by a phase factor are identified to a single point in ![]() . Colloquially, this means that we ignore global phase factors, dropping them from our calculations. The ensemble of these points form the Bloch sphere, which we introduced when discussing the fourth postulate.
. Colloquially, this means that we ignore global phase factors, dropping them from our calculations. The ensemble of these points form the Bloch sphere, which we introduced when discussing the fourth postulate.
Thanks to the time-dependent Schrödinger equation, we have found that a spin subject to a magnetic field will precess about it, a phenomenon called the Larmor precession. However, the form of the solution we have shown so far (see Eqs. 10 and 11) is not completely self-explanatory. To see show mathematically that the spin precesses in the ![]() plane, we would still need to solve the set of coupled differential equations that we came up with. In the next post, we’ll see how the time-dependent Schrödinger equation can be reformulated in a convenient way where the solution will be more obvious. Stay tuned!
plane, we would still need to solve the set of coupled differential equations that we came up with. In the next post, we’ll see how the time-dependent Schrödinger equation can be reformulated in a convenient way where the solution will be more obvious. Stay tuned!