Collapse of the wave function. Sounds intense, in’t? What does it mean? That’s the topic of this post. When we discussed the second and third postulates of quantum mechanics, we saw that, for a given physical observable , we can only measure an eigenvalue of the operator associated with . We also saw with the fourth postulate that the probability to measure this eigenvalue is given by the probability to find the quantum system in the eigenstate of associated with . The fifth postulate determines what happens to the system after we have measured .

Formulation of the postulate

Postulate V: For a system in state , immediately after measuring observable , the system is in , where is the state associated with eigenvalue , which resulted from the measurement.

In other words, the fact of measuring “projects” the system onto state . Mathematically, the projection can be represented using the projector operator ,

(1)  

Loss of information due to the measurement

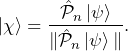
This is sometimes referred to as the collapse of the wave function because the measurement causes the system to be in one particular eigenstate of the measurement operator even if it was previously in a superposition state. Any information about the state of the system before the measurement is lost, except for the fact that the system had a non-zero probability of being in state . For example, if the system is initially in the superposition state , we know from the forth postulate that the probability of measuring the angular momentum along the axis to be is . If we do measure the angular momentum along the axis to be despite the low probability, the fifth postulate tells us that the system will then be in the eigenstate of associated with the eigenvalue , i.e., . The system is now entirely in state and the information that the system previously had a large probability of being in state is lost. In the case where the system is in a state which happens to be an eigenstate of the operator we are trying to measure (here, ), then the measurement can only result in the eigenvalue associated with the eigenstate. Then, the measurement leaves the state unchanged, and the state collapses onto itself.

Modern view

The postulates of quantum mechanics were laid down a century ago. Should modern physicists sit down and rethink the way the postulates are phrased, this one is probably the one where they would have to scratch their head the most. A century ago, measurements on quantum systems were performed very differently than what can be achieved today. For example, in a Stern-Gerlach experiment, spins in and were physically separated in space thanks to a strong magnetic field and detected using a metallic plate stopping the particles and revealing their trajectory. Here, measuring the state of the system ( or ) does disturb the system. To the contrary, modern experimental techniques have offered evidence that it is possible to detect quantum mechanical properties in much more delicate way, or in more technical terms, in a non-destructive way, meaning that it does not collapse the state of the system.

Any measurement on a quantum mechanical system requires an interface between the microscopic quantum mechanical system and the macroscopic world so that we, humans, can read it out. That’s where the difference lies between experiments in the first half of the twentieth century and what can be done now. While a Stern-Gerlach experiment brutally crushes the measured atoms on a metal plates, modern methods such as quantum sensing use quantum mechanical systems as an intermediate to measure properties of another quantum mechanical systems indirectly, minimizing the perturbation experienced by the system of interest.

Implications for NMR experiments

In modern standard NMR experiments, this postulate has limited practical implications. Yet, it is still provides insights for some experiments. Take the liquid-state NMR spectrum of a ¹³C spin J-coupled to a ¹H spin (for example in ¹³C-formate). Anyone with basic NMR knowledge knows what this spectrum looks like: it’s a doublet. In other words, two peaks separated by the J coupling value. This splitting comes from the fact that each ¹³C spin has its resonance shifted up or down, depending on the state of the ¹H spin coupled to it. In usual conditions, an individual ¹H spin does not need to be either in the or states but can be in any superposition of those, with a slight preference for the state. One could then expect that the ¹³C spins experiences a continuous distribution of field produced by the ¹H neighbor. Yet, they don’t: they see the ¹H spin either in the or state. This can be seen as the collapse of the ¹H spin state due to the interaction with the ¹³C spin that we are observing.

Do we need to measure the ¹³C spectrum for the ¹H spin wave function to collapse? No. The ¹³C spins always experiences the ¹H spin being either in the or state. So is it really the fact of performing the measurement, as we scientists perform in the lab, that cause the wave function to collapse? As far as I, the author of this post, know, this is still a question under debate in Physics and Epistemology of Science and it is certainly past the borders of my own knowledge!

Conclusion

In this post, we discussed an interesting and troubling notion in quantum mechanics: the consequence of performing a measurement. I attempted explaining how it can be understood from the NMR point of view. In the next post, we come back to more concrete grounds as we discuss how quantum mechanical systems evolve in time, according the time-dependent Schrödinger equation.