The full scripts presented in this post are available at these links: MATLAB, Python
With the first postulate of quantum mechanics, we learnt that everything there is to know about a quantum system is encapsulated in the wave function ![]() . But so far, the wave function is sort of a black box and we still need to extract relevant information from it. The second and third postulates tell us how to extract measurable quantities from the wave function. We will look at both postulates at the same time, as it’s easier to make sense of them together.
. But so far, the wave function is sort of a black box and we still need to extract relevant information from it. The second and third postulates tell us how to extract measurable quantities from the wave function. We will look at both postulates at the same time, as it’s easier to make sense of them together.
The second postulate defines the mathematical form of measurable quantities, also known as observables.
Postulate II: Every physical observable
is associated with a Hermitian operator
acting on
. The eigenvectors of
form a basis
of
.
The third postulate defines the possible outcome of a measurement of ![]() .
.
Postulate III: Measuring the observable
can only result in one of the eigenvalues of
. Because
is Hermitian, its eigenvalues are real.
Let’s say that the system is a spin in a magnetic field and I want to measure its angular momentum along the ![]() axis,
axis, ![]() . The second postulate says that this measurable quantity is associated with an Hermitian operator that we denote
. The second postulate says that this measurable quantity is associated with an Hermitian operator that we denote ![]() , where the hat represents the fact that this object is an operator acting on the Hilbert space. The third postulate adds that the result of the measurement of
, where the hat represents the fact that this object is an operator acting on the Hilbert space. The third postulate adds that the result of the measurement of ![]() can only be an eigenvalue of
can only be an eigenvalue of ![]() .
.
First, what is an operator? An operator acts on a Hilbert space by returning an element of the Hilbert space ![]() for any element of the same Hilbert space (that is, its action defines an endomorphism on
for any element of the same Hilbert space (that is, its action defines an endomorphism on ![]() ). In the matrix representation of quantum mechanics, states (kets) are represented by vectors and operators by square matrices. When the state ket is multiplied with the operator matrix, another state ket comes out. We will see in a moment what this physically means.
). In the matrix representation of quantum mechanics, states (kets) are represented by vectors and operators by square matrices. When the state ket is multiplied with the operator matrix, another state ket comes out. We will see in a moment what this physically means.
The second postulate states that operators associated with observables are Hermitian, which has important consequences. Indeed, the spectral theorem states that for any Hermitian operator ![]() , there exists an orthonormal basis of
, there exists an orthonormal basis of ![]() formed by eigenvectors
formed by eigenvectors ![]() of
of ![]() . The fact that
. The fact that ![]() is an eigenvector of
is an eigenvector of ![]() means that there exists a number
means that there exists a number ![]() , called the eigenvalue, that satisfies the eigenequation,
, called the eigenvalue, that satisfies the eigenequation,
(1) ![]()
By the third postulate, the set of eigenvalues ![]() of
of ![]() are the only possible outcomes of the measurement of
are the only possible outcomes of the measurement of ![]() . As stated in the third postulate, this eigenvalue is real because
. As stated in the third postulate, this eigenvalue is real because ![]() is Hermitian. That an operator is Hermitian means that it’s equal to its adjoint (i.e.
is Hermitian. That an operator is Hermitian means that it’s equal to its adjoint (i.e. ![]() ), which for a matrix, means that it is equal to its complex transpose. A consequence of this is that, despite the fact that the mathematical formulation of quantum mechanics involves complex numbers, measurements we perform in the lab still result in real numbers, as in classical physics.
), which for a matrix, means that it is equal to its complex transpose. A consequence of this is that, despite the fact that the mathematical formulation of quantum mechanics involves complex numbers, measurements we perform in the lab still result in real numbers, as in classical physics.
With a bit of linear algebra, one can show that, because the eigenvectors of ![]() being a basis of
being a basis of ![]() , the matrix representation of
, the matrix representation of ![]() can be written as
can be written as
(2) ![]()
where the coefficients ![]() are the eigenvalues of
are the eigenvalues of ![]() corresponding to the basis eigenvectors
corresponding to the basis eigenvectors ![]() . This property will be used below. That the eigenvectors
. This property will be used below. That the eigenvectors ![]() of
of ![]() form a basis of
form a basis of ![]() also implies that any state
also implies that any state ![]() can be written as a function of
can be written as a function of ![]()
(3) ![]()
where ![]() are normalized complex coefficients, i.e.,
are normalized complex coefficients, i.e., ![]() .
.
Let’s come back to the measurement of the angular momentum along the ![]() -axis of an isolated spin
-axis of an isolated spin ![]() . We have mentioned in the previous post that the two possible values are
. We have mentioned in the previous post that the two possible values are ![]() and
and ![]() . By the third postulate, these values are the eigenvalues of
. By the third postulate, these values are the eigenvalues of ![]() . We, therefore, have the following relations
. We, therefore, have the following relations
(4) ![]()
The matrix representation for the operator ![]() in the Zeeman basis, which satisfies the above relations is
in the Zeeman basis, which satisfies the above relations is
(5) ![]()
which can be constructed using Eq. 2.
The matrix representation of the angular momentum operators along the two other orthogonal axes are
(6) ![]()
and
(7) ![]()
which we give without proof. The three matrices used to define the angular momentum operators are called the Pauli matrices.
The three operators ![]() ,
, ![]() , and
, and ![]() that we have defined are the basic building blocks for the representation of any spin-1/2 system. To make our life easier down the line, we redefine these operators setting
that we have defined are the basic building blocks for the representation of any spin-1/2 system. To make our life easier down the line, we redefine these operators setting ![]() , not to carry this heavy factor all along. We’ll see later that this corresponds to expressing energy in terms of angular units (rad.s-1) rather than in terms of Joules. We therefore write the angular momentum operators as
, not to carry this heavy factor all along. We’ll see later that this corresponds to expressing energy in terms of angular units (rad.s-1) rather than in terms of Joules. We therefore write the angular momentum operators as
(8) 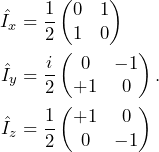
This affects their eigenvalues, which are no longer ![]() but now
but now ![]() . These operators can be constructed in a computer program using standard matrix notation.
. These operators can be constructed in a computer program using standard matrix notation.
% Definition of the angular momentum operators
Ix = [0 +1;+1 0]/2;
Iy = [0 -1;+1 0]*1i/2;
Iz = [+1 0; 0 -1]/2;# Required package for numerical calculations
import numpy as np
# Definition of the angular momentum operators
Ix = np.array([[0, +1/2],[ +1/2, 0]])
Iy = np.array([[0, -1j/2],[+1j/2, 0]])
Iz = np.array([[+1/2, 0],[0, -1/2]])noneEq. 4 shows the eigenequations for the ![]() operator, where the angular momentum expressed in SI units. Setting
operator, where the angular momentum expressed in SI units. Setting ![]() , we then have
, we then have
(9) ![]()
To the contrary, ![]() and
and ![]() are not eigenvectors of
are not eigenvectors of ![]() and
and ![]() . Indeed, we have for example,
. Indeed, we have for example,
(10) ![]()
which are not eigenquations. The eigenequations for the ![]() and
and ![]() operators can be found by diagonalizing their matrix representations and yield
operators can be found by diagonalizing their matrix representations and yield
(11) 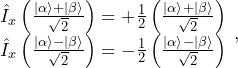
and
(12) 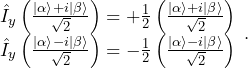
These eigenstate are sometimes defined using the following notation
(13) 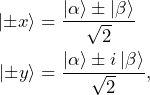
because these two states correspond to the spin having its angular momentum along the ![]() and
and ![]() axes, respectively, as we will show in the next post. The factor
axes, respectively, as we will show in the next post. The factor ![]() in the denominator ensures that the states are normalized.
in the denominator ensures that the states are normalized.
Now what does this all mean? What does it mean that a state that contains the sum or the difference of ![]() and
and ![]() ? These states are called superpositions. They are at the origin of fascinating quantum mechanical phenomena like entanglement. When the system is in state
? These states are called superpositions. They are at the origin of fascinating quantum mechanical phenomena like entanglement. When the system is in state ![]() , it is neither in the
, it is neither in the ![]() nor in the
nor in the ![]() but in a superposition of the two. This leaves us with an open question: if we have several values that can result from the measurement of same physical system, how does Nature pick which one we’ll find? We can’t answer this deep question, but the next postulate will at least tell what the probability for each measurement will be.
but in a superposition of the two. This leaves us with an open question: if we have several values that can result from the measurement of same physical system, how does Nature pick which one we’ll find? We can’t answer this deep question, but the next postulate will at least tell what the probability for each measurement will be.