Hello! In this blog post we will be introducing the nitrogen vacancy (NV) center in diamond. The NV center is an exciting physical system with potential applications in quantum information and sensing, nanotechnology, and biomedicine. Many of these applications emerge from the unique spin properties of the NV center, making it a perfect system to study at the intersection of magnetic resonance and quantum information science! To better understand these spin properties, we begin our discussion of NV centers by explaining the electronic energy structure. In particular, in this post we will see how this electronic structure allows the center to be optically spin-polarized and for the spin states to be optically read out.

Introduction to the NV Center

The NV center is composed of a nitrogen substitution adjacent to a lattice vacancy in diamond, which is a solid of tetrahedrally coordinated carbon atoms arranged in a cubic lattice. Given this diamond structure, the NV center has 4 possible orientations, each along one of the 4 crystal axes. NV centers can come in two possible charge states – NV and NV – which have different electronic structure and thus different properties. We focus on the NV center, as this charge state is at the heart of most NV applications due to the nature of its optical-spin state couplings. For ease, we will assume we are referring to this negative charge state when we say NV center.

In the negative charge state, the NV center has two unpaired electrons that form a spin pair. Figure 1 shows the electronic structure for the ground and first excited states of this system at room temperature, including the fine structure (i.e. energy dependence) for the triplet manifold. We do not account for effects from strain or magnetic fields, but these will be expanded upon in future posts.

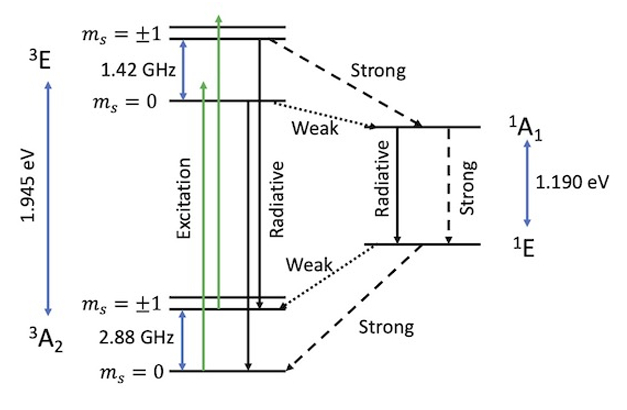
Figure 1: Diagram of the NV electronic structure and fine structure for the ground and first excited states. Triplet states are on the left side, and single states are on the right. Solid arrows in black and green indicated radiative transitions, while dashed arrows show non-radiative transitions. Blue solid arrows indicate known energy differences between different states. Note that states have been shown as two levels to emphasis there are two distinct states. However, at zero field these states will have the same energy.

Triplet State Energies

While this diagram may at first seem hectic, we will go through each of the different levels and transitions to explain the important aspects of the system. Firstly, we note that these energy levels are not drawn to scale, but the magnitude of significant transitions are marked. We begin by focusing on the triplet manifold on the left side. We see (excluding the fine structure, i.e. the different states) that there are two energy levels, with term symbols and . The superscript 3 describes the spin multiplicity of the system, here 3 since these states have . (Spin multiplicity is , which is the total number of states for a given spin , where states are the possible spin projections along the quantization axis). The terms and come from group theory and define the symmetry of the electronic wavefunctions. The ground and first excited states have an energy gap of 1.945 eV, equivalent to light with a wavelength of 637 nm.

Within the ground state, we point out the zero-field splitting (ZFS) between between the and states of 2.88 GHz. A similar ZFS occurs for the excited state, where the magnitude of the ZFS is 1.42 GHz. Zero-field splitting is so named because it causes differences in energies, even in the absence of a magnetic field. This splitting emerges from magnetic dipole interactions between the two electron spins. The presence of this ZFS allows for spin transitions, even in the absence of a magnetic field. Thus we are able to conduct magnetic resonance experiments without an external field!

Excited State Decay

Next we consider optical excitation within the triplet manifold from the ground state into the excited state. While the energy difference between these states is 1.945 eV, photons with higher energy can also excite this transition (where the extra energy excites vibrational modes). In this case the extra energy will be thermally dissipated, and the resulting state will be the same. Since green lasers are common in NV experiments, we have marked these excitations in green, and displayed them as exciting to an energy slightly higher than the final state (after thermal dissipation). The excited states can then undergo radiative decay, releasing photons with energy 1.945 eV and returning to the ground state without changing the state. This process of photon absorption and subsequent emission is known as photoluminescence. As we shall see, this is a key feature that makes the NV center so useful in various applications.

The excited state can also undergo non-radiative decay into the excited singlet state. In this case, instead of releasing energy in the form of photons, i.e. quantized light particles, energy is released in the form of phonons, i.e. quantized vibrational excitations of the lattice. This process, where the spin multiplicity of the electronic state changes, is known as intersystem crossing, and is enabled by spin-orbit coupling, the coupling of an electron’s spin state to its orbital motion. The singlet states are on the right hand side of Figure 1, with term symbols and . We note that there are two singlet states, with a difference of energy 1.190 eV. From the excited singlet state, the system can relax via either radiative or non-radiative transitions to the singlet ground state. In the case of radiative decay, the process emits an infrared photon with wavelength of 1042 nm. Either decay pathway leads to the singlet ground state, from which the non-radiative process of intersystem crossing relaxes the electrons back into the triplet ground state.

Implications of Different Decay Pathways

Critically, the non-radiative decay processes are not all equally likely. Rather, as marked in Figure 1, some of these processes are stronger, i.e. more likely to occur, than others. From the excited triplet state, the state is more likely than the state to decay into the excited singlet state. The singlet ground state is then more likely to decay into the than the states. Therefore, while the photoluminescence pathway in which the triplet ground state is excited and radiatively decays will conserve the m_s state, this non-radiative pathway via the singlet state preferentially converts the states into the state. Therefore, by continually exciting the NV system with a laser, we can increase the population of our state. This process is known as optical pumping, and allows us to polarize the spin state of our NV center, even without an external magnetic field.

One additional feature that comes from the different strengths for the non-radiative decay pathways is that the state is more likely to relax via a radiative process than the states. The state is thus the “light” state and the states are the “dark” states. Therefore, by measuring the fluorescence intensity after exciting the NV center, one can measure the electronic spin state. (More specifically, we can measure the relative population of the , but cannot measure the difference in populations between and .) This technique is the basis for optically detected magnetic resonance (ODMR), and a more detailed discussion can be found in here.

Conclusion

In this post, we have provided a fundamental background on the electronic structure of the NV. Amazingly, we have seen that by consideration of different excitation and decay processes, we are able to understand both optical spin polarization and optical spin read out! These features are key to various applications of the NV center, such as ODMR, dynamic nuclear polarization methods, masers (the microwave “cousin” of the more common laser), and single molecule magnetic resonance. Future posts will dive into all of these areas, as well as other potential applications for the NV sensor in quantum sensing and quantum information, so we hope the reader will stay tuned!