Hello! Today, I want to introduce SpinDrops, a unique tool for the visualization of small spin systems. SpinDrops is a free software for simulating spin 1/2 systems of up to three spins, and can be downloaded or run via a web app. Here, and in future posts that build off this introduction, I will present my take on SpinDrops, and where I have found it to be useful for simulating spin systems and building physical intuition.
Right off the bat, I want to emphasize that SpinDrops is a tool developed by the Glaser group at the Technical University of Munich, and give them credit for developing such an amazing tool for understanding and visualizing spin systems. I highly recommend checking out their SpinDrops website, which includes information on downloading the software, as well as an abundance of resources to familiarize users with the software and the mathematical background on the representation scheme.
To visualize spin systems, SpinDrops uses the DROPS representation, originally developed in a 2015 paper by Garon et al. The DROPS representation provides an intuitive method for displaying spin operators in the form of three-dimensional “droplets.” The shape, color, and orientation of these droplets will be defined by the spin operators they are displaying, i.e. 
, 
, or 
, as shown in Figure 1. For those who are interested in a full understanding of the mathematics behind these droplet representations, I recommend reading the 2015 paper linked above. However, I do not feel the detailed (and somewhat complicated) mathematics behind the DROPS representation are fully necessary to utilize SpinDrops to visualize spin operators and use the tool to build one’s understanding of small spin systems. Here, I will simply mention that the general approach is to decompose each spin operator into a sum of tensor operators, which can then be mapped to the spherical harmonics and visualized in three dimensions. In the future, look out for a post that goes deeper into the mathematics behind the DROPS representation.
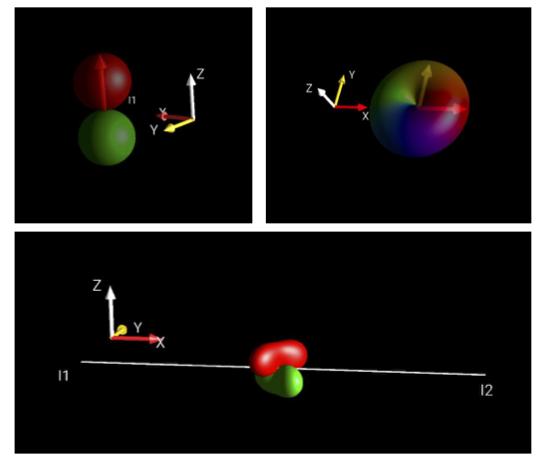
. Top right: . Bottom: . Some of you may be asking why we would want to visualize systems of 1, 2, and 3 spins, given that there is a perfectly good mathematical description of them in the form of the density matrix. While this is true, I believe visualization is a powerful tool for developing intuition for physical systems, and for many learners may be a much more natural way to understand spin dynamics than a purely mathematical representation. Also, SpinDrops will display other representations, such as the density matrix or product operator decomposition, to help draw links between the visual and mathematical approaches. For me, even though I do not necessarily consider myself a highly visual learner, I found SpinDrops to be a highly useful (and fun) tool to build my fundamental intuition of small spin systems and different pulse sequences.
While this post isn’t a full SpinDrops tutorial (a tutorial can be found on the SpinDrops site), I did want to give a sense of how to start exploring with SpinDrops. Personally, I found that once I figured out these basics, the best way to learn the program was just to explore the different functionalities on my own.
Setting up the spin system: To set up your spin system, go to the Spin System tab in the menu at the top left and select your option – 1-Spin, 2-Spin, 3-Spin chain, or 3-Spin triangle (The two 3-Spin options have identical functionalities but just slightly different visuals). Then select Parameters within the same tab – this will pop up a window that allows you to adjust the offset frequency of each spin as well as the couplings between them. Note that by clicking the Advanced button, additional options appear. One can set the system to be in the strong coupling regime (a future post in the Theory section will explore the strong vs. weak coupling regimes if you’re interested in learning more), as well as selecting whether you have a homonuclear or heteronuclear spin system by toggling between the f0 and f1 options (essentially, will pulses excite all spins or a specific spin(s)).
Setting the initial state: Open the Initial State tab in the menu. A number of default options will appear, with the exact options depending on the number of spins in your system. You can also input any arbitrary initial state by selecting the Graphical Edit… or Textual Edit… options. For me, if my desired initial state isn’t one of the default options, I like the Textual Edit… option. Here, initial states can be input in the form of product operators – for instance, I1x + I2x for two spins aligned along the x-axis, or I1z + 4*I2z for an initial population state with spin 2 having four times the polarization of spin 1 (useful for visualization a sequence such as 
H-
C INEPT). Or states can be input as a density matrix in bra-ket form – for instance, (|01>-|10>)*(<01|-<10|) will create a spin singlet state.
Selecting a pulse sequence: Open the Pulse Sequence tab in the menu. Again, a number of default options will appear, such as rotations, delays, and spin echoes. Additionally, one can select from several predefined homonuclear and heteronuclear pulse sequences, or explore the tutorial sequences on topics ranging from phase cycling to implementing quantum gates. Users can also create their own arbitrarily complex sequences, including spin selective pulses and delays, with the Edit Sequence option. Both the preset sequences and user defined sequences are great learning tools for developing an understanding of new pulse sequences and how they act on each spin in the system.
Tools in the View menu: Last, but certainly not least, are the tools available in the View tab in the menu. By selecting options such as List Prod. Ops… or Density Operator…, one can view the mathematical product operator state or density matrix alongside the DROPS visuals – comparing across them is a great method to develop intuition on the relationship between the visual and mathematical representations. Addition tools include allowing users to visualize the matrix representation of the Hamiltonian or propagator during each portion of the pulse sequence, or to visualize the evolution of coherence orders on each spin in the Separation tab.
Running the experiment: Now you’re all set up to run your experiment! Click the “Play” button to run the experiment. You can use the different options in that bar to slow down or speed up the experiment, as well as jumping between the different blocks of the sequence.
While SpinDrops is already an amazing tool, it does have some current limitations (some of which are being addressed for future versions of the software). Of course, one limitation is that the maximum system size is three spins. However, there is a lot of fundamental spin physics that can be explored with three-spin systems! A more significant limitation would be that currently there is no relaxation implemented in SpinDrops – although this may be included in future additions. As such, concepts in relaxation and experiments that rely on relaxation cannot be explored in SpinDrops. On a related note, spontaneous events such as 2 spin flip-flops, where spins with equal energy but opposite alignment swap alignments are also not included. Nevertheless, SpinDrops allows for a huge range of experiments and concepts in magnetic resonance and quantum computing to be explored.
To finish up this introductory post, we will walk through an example pulse sequence – let’s start with a spin echo sequence with a pair of weakly coupled spins. To set this up, we start with a 2-spin system with different offset frequencies and non-zero J-coupling – let’s say 0.7 Hz (just make sure you haven’t clicked the strong coupling option). Then, let’s set our initial state to I1z + I2z – both spins are polarized along the z-axis, as we would have at the start of a magnetic resonance experiment. Finally, we can go to the Pulse Sequence tab and select 90
– T – 180 – T >> Echo T = 1/(4*J12). This option ensures that the delay of our echo is optimized so that our final state is pure 2-spin antiphase pattern. Before running the sequence, I like to open the product operator and density matrix representations to view alongside the DROPS visual evolution. Now, hit run! You should see something similar to the video below. Note that our final shape is a four-lobed object in the y-z plane – comparing to our product operators, we see that this is the sum of I1zI2y and I1yI2z antiphase operators. From here, you are ready to start exploring SpinDrops. You can play around with this sequence, for instance you can see how the sequence breaks down if you go into the strong coupling regime, or if you change your echo delay time so that it is not optimized for the J-coupling between the spins, or you can start investigating other sequences.
Hopefully, this brief introduction to SpinDrops has excited you to further explore this incredible tool for spin system visualization. While this post gives you the basic tools to get started, the best way to learn more about SpinDrops is to explore its features on your own! I think that SpinDrops has great potential for both beginners and experts in magnetic resonance, for building physical intuition, understanding pulse sequences, and adding a visual element to teaching what are sometimes very mathematically-heavy ideas. Keep an eye out for future post series on SpinDrops, exploring ideas such as fundamental pulse sequences, pulsed DNP, and the implementation of simple quantum computing algorithms!